Random research highlights
Topological bosonic states via squeezing (2016)
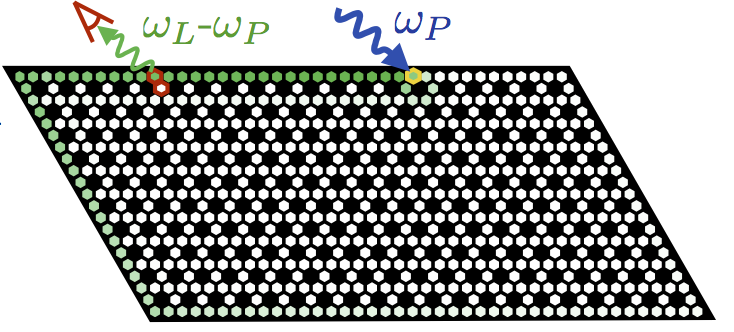
There is enormous interest in engineering topological photonic systems, where topological protection guarantees the existence of robust edge modes. Most works in this field amount to replicating a well-known fermionic single-particle Hamiltonian. We recently studied a class of systems where this correspondence fails. Here, topology is induced by coherent two-photon driving (i.e. parametric driving). While these systems have a Hamiltonian resembling that of a fermionic topological superconductor, the bosonic physics is completely different. In particular, the topologically-protected edge states can act as frequency-converting channels, and can even serve as quantum-limited amplifiers and squeezed light sources.
Non-reciprocal interactions via dissipation engineering (2015)
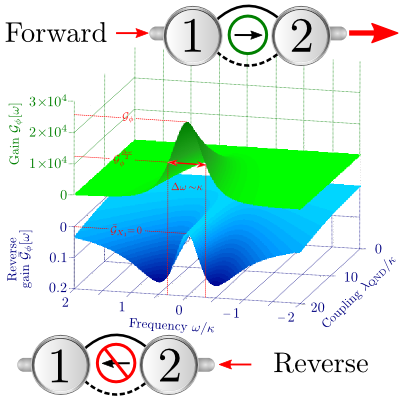
Can we make two systems A and B interact with one another, so that system B is influenced by system A, but system A is completely insensitive to B? We recently devised a very general way to construct such "non-reciprocal" interactions, by having both systems talk to a dissipative environment in just the right way. Our approach doesn't rely on magnetic fields or magnetic material, and could be used to construct new kinds of directional quantum microwave and photonic devices. Implenting these kinds of interactions on a lattice could also lead to a range of unique quantum phases.
Quantum back-action evasion (2014)
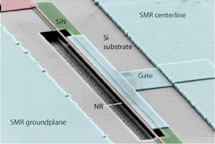
In quantum mechanics, Heisenberg uncertainty places a fundamental limit to how well one can make a continuous position measurement. This is because of the "back-action" of the measurement: crudely speaking, measuring something necessarily messes up its state. We have recently studied a scheme which allows one to surpass this standard Heisenberg limit; we also showed how this scheme leads to so-called "squeezed" states of mechanical motion. These ideas were realized in recent experiments by the Schwab group at Caltech (we provided the theory).
Quantum dots, phonons & back-action (2012)
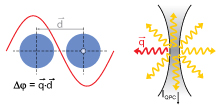
A common way to measure information in quantum-dot qubits is to use the current through a nearby quantum conductor (a quantum point contact) as a detector. Quantum mechanics tells us that any time we look at a system, we must somehow disturb it (this is back-action), and this scheme is no different. Experimentalists both at NRC Ottawa and the LMU in Munich recently observed a striking effect where the back-action disturbance strongly oscillated as a function of quantum dot energy level spacings. We were able to explain this in terms of quantum interference and a phonon-mediated back-action effect. A joint experiment-theory paper recently appeared in Nature Physics.
Interference, optomechanics & state transfer (2012)
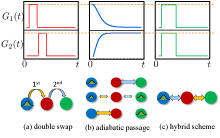
Several groups are interested in the possibility of transferring quantum states between very different kinds of systems, using a mechanical resonator as an intermediary (e.g. between a superconducting qubit and optical photons). A potential problem is dissipation originating from the mechanical resonator, which could damage the state being transferred. We recently proposed methods for combatting these effects via interference: one can effectively use the mechanical resonator to transfer a state, without ever having the state actually in the resonator! This is the optomechanical analogue of a well-known protocol in atomic physics (STIRAP).
Strongly-coupled electromechanics (2010)
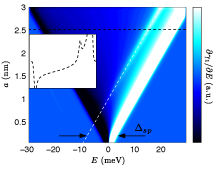
A quantum electromechanical system consists of a mechanical resonator (i.e. a vibrating beam) coupled to some sort of interesting quantum electronic conductor. An interesting regime of these systems is where the coupling becomes so strong that the mechanical motion nonlinearly affects the conductor. Usually this regime is difficult to treat theoretically, and even harder to achieve experimentally. In a collaboration with the Grutter experimental group at McGill, we studied an atomic force microscope cantilever capacitively coupled to the charge on a self-assembled quantum dot in the strong coupilng regime. Electrons tunneling on and off the dot cause damping of the cantilever motion; we demonstrated how this damping can be used to directly probe the energy levels of the dot.
A new kind of cavity optomechanics (2009)
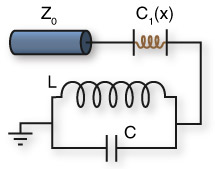
There is has been a remarkable amount of progress in using driven optical and microwave resonators to make quantum measurements of micron-scale mechanical structures. The usual setup is that the frequency of the resonator depends on the mechanical position. We recently developed a theory of dual version of this system where the mechanical element now modulates the coupling of the resonator to the dissipative bath which both drives and damps it. Remarkably, interference effects are important in this system, leading to a number of surprising & useful quantum back-action effects.
Read the paper (Physical Review Letters)
Recent experment from the Tang group at Yale on this system